OBSERVER FRAME AND SPEED OF LIGHT

We're moving on to the second stage of uncovering/proving the formula E = mc². Except for the proof of E=mc², which I'll be publishing recently, this and future texts won't be as mathematical as the MOMENTUM text, but you'll still need to strain your brain. After all, we're following the path of Einstein's famous formula, and let that path be a bit challenging, right? spent decades to find these formulas As a reward, when you listen to my texts carefully and understand them fully, you will fully understand why the time of moving objects slows down.

The statement that the speed of light is constant might seem like nothing special at first glance, because the constancy of the speed of light can be likened to a car always traveling at the same speed. What significance does it have that light always travels at the same speed? You're right! There's a flaw in my statement. Correctly, I should have said:

The speed of light is the same in every frame of reference!

This statement completely changes everything! Now, of course, we need to explain what "frame of reference" means. This concept is obviously named after humans (in terms of the observer), but the frame of reference applies not only to humans but also to any object. Accordingly, every living or non-living object (we'll generally call it an "object") has a frame of reference within it. Two or more objects can be in the same frame of reference. So, what's the difference between one frame of reference and another? This is a question that can be easily answered, yet still difficult to grasp. The only difference between two frames of reference is their different states of motion relative to each other. In other words, if two objects are at rest relative to each other, they are in the same frame of reference; otherwise, they are in different frames of reference.

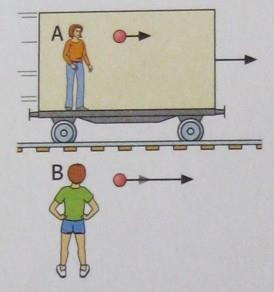Example (see the picture): Two people are standing at a train station, like Person B in the picture. A train is passing by them at a certain speed. Let's count the frames of observation in this scene: If two people waiting at the train station are standing still, they are in the same frame of observation. Simultaneously, the train station, the tracks, and simply the entire world are in the same frame of observation as these two people because they are stationary relative to each other. However, the train and its passengers are not in the same frame of observation as those waiting at the station; they are in a different frame of observation. The train and its passengers are in motion relative to the train station, and this motion places them in a different frame of observation because the train and its passengers, like Person A in the picture, are in motion relative to those waiting outside. Because the train, its passengers, and all objects inside the train are in the same motion relative to those inside the station, they are in a different frame of observation. In other words, there are two frames of observation in this scene: one containing those waiting at the station, and the other containing the train and its passengers. When I say the same "state of motion," I mean not only that their speeds are the same, but also that their directions are the same. Because, imagine, a train is approaching from the opposite direction on the other track. Even if the trains are traveling at the same speed, because their directions are opposite, in classical physics, they would move at twice their relative speed. In other words, it's impossible to speak of the same frame of observation. This means that both the speeds and directions (i.e., their states of motion) of two objects must be the same for them to be in the same frame of observation.

As you can see, there are an infinite number of frames of observation. The slightest change in speed or direction, in principle, means a different frame of observation. For example, even when you're walking down the street, your feet are often in different, constantly shifting frames of observation compared to your body and head, because you're swinging your feet back and forth as you walk, but your body is constantly moving forward.

Now, in light of this information, let's revisit the sentence I wrote above: The speed of light is the same in every frame of observation! So, no matter how you move, when you measure the speed of a given beam, you'll always find the same constant speed. This speed is approximately three hundred thousand kilometers per second. Some of you may not yet fully grasp what this means. So, let's give another example:

Let's add something to the scene in the example I gave above. Let's place a light tower a short distance from the train station, in the direction the train is traveling, and turn on the tower's light. This light will naturally radiate in all directions and, as mentioned above, travel at 300,000 kilometers per second relative to the tower. So, what is the speed of light for those waiting at the station? Since those waiting at the station are stationary relative to the tower, the light will naturally reach them at 300,000 kilometers per second. In other words, those at the station will measure the speed of light as 300,000 kilometers per second. What will the speed of light be for those traveling on the train? As I mentioned, since the tower is in the train's direction of travel, the train and its passengers are traveling toward the light emitted by the tower. Conventional thinking requires train passengers to estimate the speed of light not as 300,000 kilometers per second, but as a speed greater than that, because the speed of the train is added to the speed of light. However, according to the sentence "The speed of light is the same for every frame of observation," those traveling on the train will perceive the speed of light as 300,000 km/h! In this case, the train's speed is irrelevant. In other words, even if the train were traveling at 200,000 km/h toward the light, the light would still be 300,000 km/h for the passengers. Or, even if the train were traveling in the opposite direction—in other words, in the direction the light is traveling—the train passengers would be running away from the light in this case, but even in this case, the passengers would perceive the speed of light as 300,000 kilometers/sec. Here, too, the speed of the train is irrelevant. The speed of light is always 300,000 km/h for every object and every state of motion (i.e., every frame of observation)!

This phenomenon has only been discovered experimentally. Einstein's genius lies in his accurate interpretation of this phenomenon and its inclusion in his calculations. The most prominent physical truth Einstein discovered based on the constancy of the speed of light is the equation E=mc². So, how can we understand and explain this strange property of the speed of light, which is completely contrary to our daily experiences? If you continue to follow my series of articles, I'll explain everything! Thank you!

 Author: İlker Savas