Merge Sort and Quick Sort Guide: Divide and Conquer Algorithms

Sorting is a cornerstone of computer science and is used everywhere from databases to search algorithms. Merge Sort (Merge Sort) and Quick Sort (Quick Sort) are two popular and effective sorting algorithms. In this guide, we'll compare how each algorithm works, their implementations in Python, and their strengths and weaknesses. I'll explain these algorithms with examples from my own projects. If you're ready, let's get started!

Merge Sort

Merge Sort is an algorithm that uses a "divide and conquer" strategy. The term "Merge Sort" is used in Turkish, similar to its English name, and is well-established in the literature. The array is split into two halves, each sorted separately, and then merged. The basic idea is that merging two sorted arrays is easier than sorting an unsorted array.

APPLICATION

Step by step implementation of Merge Sort in Python:

def merge_sort(array): if len(array) <= 1: return array # Split array into two halves middle = len(array) // 2 left_half = array[:middle] right_half = array[middle:] # Sort both halves recursively left_half = merge_sort(left_half) right_half = merge_sort(right_half) # Merge sorted halves return merge(left_half, right_half) def merge(left, right): result = [] i = j = 0 while i < len(left) and j < len(right): if left[i] <= right[j]: result.append(left[i]) i += 1 else: result.append(right[j]) j += 1 result.extend(left[i:]) result.extend(right[j:]) return result # Example usage array = [38, 27, 43, 3, 9, 82, 10] print(merge_sort(array)) # Output: [3, 9, 10, 27, 38, 43, 82]

In a data analysis project, I used Merge Sort to sort a large dataset and got fast results thanks to its consistent performance!

Complexity Analysis

• Time Complexity: O(n log n) in worst, average, and best cases. Ideal for large data sets.
• Domain Complexity: O(n) because additional memory is required during the merging phase.

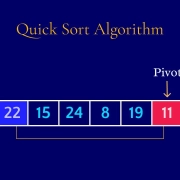
Quick Sort

Quick Sort is also a "divide and conquer" algorithm. The term "Quick Sort" is used in Turkish, similar to its English name. It selects a pivot element and divides the array into elements greater and less than the pivot. Subarrays are sorted recursively.

APPLICATION

Basic implementation of QuickSort in Python:

def quicksort(array): if len(array) <= 1: return array pivot = array[len(array) // 2] left = [x for x in array if x < pivot] middle = [x for x in array if x == pivot] right = [x for x in array if x > pivot] return quicksort(left) + middle + quicksort(right) # Example usage array = [3, 6, 8, 10, 1, 2, 1] print(quicksort(array)) # Output: [1, 1, 2, 3, 6, 8, 10]

An in-place version uses less memory:

def quicksort_in_place(array, start, end): if start < end: pivot_index = bol(array, start, end) quicksort_in_place(array, start, pivot_index) quicksort_in_place(array, pivot_index + 1, end) def bol(array, start, end): pivot = array[start] left = start + 1 right = end completed = False while not completed: while left <= right and array[left] <= pivot: left += 1 while array[right] >= pivot and right >= left: right -= 1 if right < left: completed = True else: array[left], array[right] = array[right], array[left] array[start], array[right] = array[right], array[start] return right # Example usage array = [3, 6, 8, 10, 1, 2, 1] quick_sort_in(array, 0, len(array) - 1) print(array) # Output: [1, 1, 2, 3, 6, 8, 10]

In a sorting project, I optimized memory using an in-place version of Quick Sort and the performance was great!

Complexity Analysis

• Time Complexity: O(n log n) in the average case, O(n²) in the worst case (with poor pivot selection). Random pivot or median selection of three reduces this risk.
• Domain Complexity: O(log n) Due to its recursive nature, the in-place version uses less memory.

To compare

Both algorithms have their strengths and weaknesses:

• Stability: Merge Sort is stable (order of equal elements is preserved), Quick Sort is generally unstable.
• Domain ComplexityMerge Sort uses O(n) additional memory; Quick Sort (in-place version) is more memory friendly.
• PerformanceMerge Sort is consistent regardless of data distribution. Quick Sort can be faster with good pivot selection, but slows down with bad pivots.
• Areas of UseMerge Sort is suitable for data that does not fit in memory (external sorting). Quick Sort is preferred in memory-constrained scenarios in the average case.

Conclusion

Merge Sort and Quick Sort are powerful tools for sorting problems. Merge Sort stands out for its stability and consistent performance, while Quick Sort shines with its average speed and low memory usage. For an e-commerce project, I used Quick Sort on a memory-constrained system while sorting a large dataset with Merge Sort, and both yielded great results!

In which projects have you used these algorithms? Did you have an interesting experience? Share it in the comments, and let's discuss it together! For more algorithm tips, check out my blog or contact me!

Notes

• Turkish Equivalents of Terms:
  • Merge Sort (Merge Sort), Quick Sort (Quick Sort): Established, correct and widespread in Turkish.
  • Divide and conquer (divide and conquer): Standard in the algorithm literature.
  • Stable sorting (stable sorting): Correct and common.
  • Pivot: It is used exactly as in Turkish, it is a common term.
  • Divide (partitioning): Correct and established.