Bilgisayar Bilimi Temelleri: Binary Sistemden Algoritmalara

Computer Science While fundamentals is often perceived as a field reserved for software developers or technology experts, it's actually a discipline anyone can learn and integrate into their daily lives. At its core lies the approach to identifying, analyzing, and effectively solving a problem. This provides benefits in many areas, from acquiring new skills to bringing an analytical perspective to everyday problems. If you're looking to delve into the fundamentals of computer science, this article is for you. We'll explain the fundamental concepts for beginners and deepen the topic with practical examples.

Fundamental Structure of Computer Science: Input, Algorithm and Output

Computer science is built on three fundamental pillars: Input (data entry), Algorithm (problem-solving logic), and Output (data output). This structure is essentially based on a philosophical foundation; it proceeds through logical steps, similar to Aristotle's rules of logic. It takes a problem, breaks it down, processes each part in a logical order, and produces a result.

This approach makes the fundamentals of computer science accessible. For example, even a coffee machine operates on this principle: coffee beans and water (input), the brewing process (algorithm), and instant coffee (output). So how do computers understand and process this data? The answer lies in the binary number system.

Representing Data: Binary Systems and Transistors

Computers represent everything using the binary number system: 1 and 0. These numbers are physically implemented through transistors. Transistors, found in billions in processors, represent the states of "powered" (1, on) or "powered off" (0, off). These transitions form the basic unit of data storage and processing.

So how do simple 1s and 0s turn into complex data? Imagine representing numbers with one hand. You normally count from 1 to 5 with five fingers. But if you assign powers of two to each finger (1, 2, 4, 8, 16), you can add up to 31 in combinations. For example:

First finger (1) + Second finger (2) = 3
All fingers = 1 + 2 + 4 + 8 + 16 = 31

Computers work similarly. A single 1 or 0 bit (Binary Digit). Eight bits come together to form byte and provides 256 different possibilities (0-255). This is based on place values as in the decimal system:

In decimal system: 123 = (1 × 10²) + (2 × 10¹) + (3 × 10⁰) In binary system: 101 = (1 × 2²) + (0 × 2¹) + (1 × 2⁰) = 5

This base is used to represent numbers and also letters and colors.

Numbers, Letters, and Colors: Coding Systems

Limiting yourself to 256 possibilities is insufficient for letters. Here it is ASCII (American Standard Code for Information Interchange) comes into play. Each byte represents a character:

01000001 = 65 = 'A'
01100001 = 97 = 'a'

However, ASCII is suitable for limited alphabets like English. It is insufficient for Turkish 'ç', 'ş' or Chinese characters. To solve this problem Unicode Advanced systems such as these have been developed that cover millions of characters using 16, 24 or 32 bits.

For colors RGB The (Red-Green-Blue) model is used. Each color is represented by three bytes: Red, Green, and Blue intensities (0-255 each). This produces 256 × 256 × 256 = 16,777,216 colors. For example, pure red: (255, 0, 0). This system plays a fundamental role in everything from digital images to web design.

When learning computer science fundamentals, understanding these encodings helps you grasp how data is stored and processed.

What is an Algorithm? Detailed Instructions and Misunderstandings

AlgorithmA step-by-step solution to a problem is described. However, computers can't reason like humans; every detail must be specified. This is the most misunderstood part of computer science fundamentals. People think the algorithm is simple, but they forget that the person you're dealing with is a "dumb" machine.

Let me give an example of a dialogue between me and a friend:

I: Tell me how to brew tea as an algorithm.
My friend: Take the teapot.
I: Ok.
My friend: Fill it with water.
I: Into what?
My friend: Into the teapot of course!
I: I'm a machine, I can't judge. I just took it, but I don't know what to do with it.
My friend: Light a fire on the stove and put the kettle on.
I: Okay, but the fire is out.
My friend: From where?
I: You said to fill it with water, but you didn't say how much. It overflowed and put out the fire.

The conclusion: “Wow, do I have to plan everything down to the smallest detail?” Yes, that’s exactly what an algorithm is! In computer science fundamentals, instructions must be clear and complete.

Practical Example: Phonebook Search Algorithms

Now let's solve a problem: Find the number of "Erhan Kılıç" in a 1000-page phone book.

Linear Search Algorithm (Simple but Inefficient):

Open the notebook.
Check each page in turn.
Write down the number if you find it, otherwise move on.

This scans 1000 pages in the worst case – inefficient!

Binary Search Algorithm (Efficient):

Open the notebook from the middle page.
Is the person you're looking for on that page? If so, enter the number.
If not, in alphabetical order (e.g. for the letter E): If you passed, discard the right side, if not, discard the left side.
Turn to the center page with the remaining notebook, repeat.

This method makes the search logarithmic – a maximum of 10 steps in a 1000 page notebook!

Try it yourself: Apply this algorithm to a book and share it in the comments. Ask any questions!

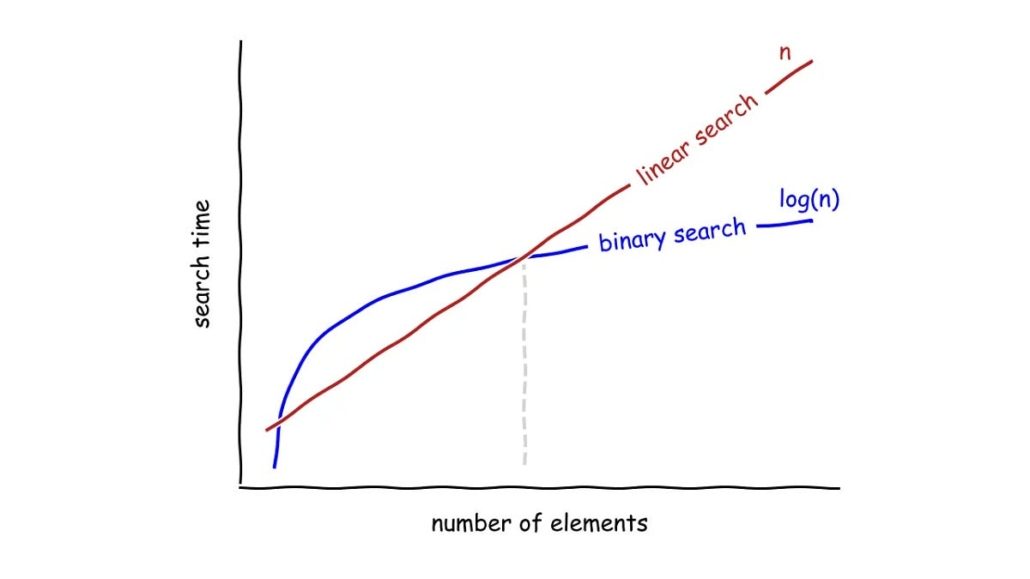
Algorithm Efficiency: Time and Complexity

The algorithm should not only be accurate, it should also be efficient. Efficiency, time complexity measured by: How does the solution time change as the problem size (n, e.g., number of pages) increases?

Linear search: O(n) – Directly proportional, graph straight line.
Binary search: O(log n) – Logarithmic, growth slows down.

Let's visualize this difference:

Linear & Binary Search Algorithms | by Mehmet Akif Özgür | Medium

As the graph shows, binary search gets much faster as n gets larger. In computer science fundamentals, these concepts (Big O notation) will be deepened in the following lessons.

Computer science fundamentals will improve your problem-solving skills and make your life easier. This article is an introduction; we'll cover more in subsequent articles.

0 0 votes

Article Rating