A Guide to Big O Notation: Understanding Algorithm Efficiency
The efficiency of algorithms is critical in the world of computer science and programming. Imagine two different methods solving the same problem; both might produce the correct result, but one might be much slower than the other. Here's how Big O Notation This is where it comes in. This tool for measuring and comparing algorithm performance is our guide to designing efficient solutions. In this article, we'll explore what Big O Notation is, why it's important, and how to interpret it. I'll explain this concept to you using examples from my own experience. If you're ready, let's get started!
Basic: What is Big O Notation?
Big O Notation is a mathematical way to describe the performance or time complexity of an algorithm. The term "Büyük O Notasyon" (Big O Notation) is used in Turkish, similar to its English name, and is well-established in the literature. It shows how the algorithm's running time varies depending on the input data size (n). Simply put, it answers the question: "How does the algorithm's running time increase as the input data size increases?"
As an example, consider searching for an element in an array. Linear Search (Linear Search) scans the array one by one and continues until the target element is found. This algorithm Front) has a time complexity of n, where "n" is the number of elements in the array.
def linear_search(array, target): for element in array: if element == target: return True return FalseHowever, not every algorithm operates linearly. Big O notation allows us to classify algorithms based on input size and helps us understand which algorithm is more efficient.
Notation: Parsing Symbols
Big O Notation is expressed with symbols and terms that can seem intimidating at first glance. Let's examine the most common ones:
1. O(1) – Constant Time Complexity
Constant-time algorithms take the same amount of time regardless of the input size. For example, removing an element from an array by its index:
def element_access(array, index): return array[index]Whether the array has 10 elements or 1,000 elements, this operation is completed in constant time.
2. O(log n) – Logarithmic Time Complexity
Logarithmic algorithms halve the input data at each step. Binary Search (Binary Search) is a classic example of this. As the input grows, the number of steps increases logarithmically.
def binary_search(array, target): left, right = 0, len(array) - 1 while left <= right: middle = (left + right) // 2 if array[middle] == target: return middle elif array[middle] < target: left = middle + 1 else: right = middle - 1 return -1In a database project, I quickly searched a sorted list using Binary Search and the results were incredibly fast!
3. O(n) – Linear Time Complexity
Linear algorithms operate proportionally to the input size. For example, calculating the sum of an array:
def linear_sum(array): sum = 0 for element in array: sum += element return sumIf the input size is doubled, the runtime approximately doubles.
4. O(n log n) – Linear-Logarithmic Time Complexity
Algorithms like Merge Sort and Quick Sort fall into this category. They are slightly slower than linear algorithms but much faster than quadratic algorithms.
def merge_sort(array): if len(array) <= 1: return array middle = len(array) // 2 left_half = array[:middle] right_half = array[middle:] left_half = merge_sort(left_half) right_half = merge_sort(right_half) return merge(left_half, right_half) def merge(left, right): result = [] left_index, right_index = 0, 0 while left_index < len(left) and right_index < len(right): if left[left_index] < right[right_index]: result.append(left[left_index]) left_index += 1 else: result.append(right[right_index]) right_index += 1 result.extend(left[left_index:]) result.extend(right[right_index:]) return result5. O(n²) – Quadratic Time Complexity
Quadratic algorithms work proportional to the square of the input size. For example, Bubble Sort (Bubble Sort):
def bubble_sort(array): n = len(array) for i in range(n): for j in range(0, n - i - 1): if array[j] > array[j + 1]: array[j], array[j + 1] = array[j + 1], array[j]If the input size is doubled, the running time quadruples. While this isn't a problem for small datasets, it can be slow for large datasets.
6. O(2^n) – Exponential Time Complexity
Exponential algorithms grow exponentially with the input size. For example, recursive Fibonacci computation:
def fibonacci_rekursif(n): if n <= 1: return n return fibonacci_rekursif(n - 1) + fibonacci_rekursif(n - 2)Such algorithms become unmanageable with large inputs.
7. O(n!) – Factorial Time Complexity
The slowest algorithms grow at factorial speed. For example, generating all permutations:
def create_permutation(elements): if len(elements) == 1: return [elements] permutations = [] for i, element in enumerate(elements): remaining_elements = elements[:i] + elements[i+1:] for perm in create_permutation(remaining_elements): permutations.append([element] + perm) return permutationsThese algorithms are so slow that they should generally be avoided.
Big O Notation in Real Life
Big O Notation isn't just a theoretical tool; it's also crucial for practical decisions. When choosing an algorithm for a sorting problem, Big O Notation guides you. For example, a quadratic algorithm might be fast on a small array, but O(n log n) algorithms make a difference on large datasets. For an e-commerce project, I used Merge Sort to sort a large list of products, and the performance was fantastic!
Hidden Factors: Domain Complexity and the Real World
Big O Notation generally focuses on time complexity, but field complexity It's also important. In Turkish, "space complexity" is a standard term. Some algorithms can be problematic on devices with limited memory. Furthermore, real-world conditions such as programming language, hardware architecture, and constant factors influence algorithm selection. Big O offers a general overview, but it's not an absolute guarantee.
Conclusion
Big O Notation is a powerful tool for analyzing and comparing the efficiency of algorithms. It allows algorithms to be classified based on their input size, empowering programmers to make informed decisions. However, real-world conditions and practical constraints must also be considered. In a data analysis project, I optimized performance by selecting the right algorithm using Big O Notation. Use this notation as a guide and design efficient solutions!
In which projects have you used Big O Notation? Did you have an interesting experience? Share it in the comments, and let's discuss it together! For more algorithm tips, check out my blog or contact me!
Notes
- Turkish Equivalents of Terms:
- Big O Notation (Big O Notation): Established, correct and common in Turkish.
- Time complexity (time complexity), field complexity (space complexity): Standard in the algorithms literature.
- Linear search (linear search), binary search (binary search), bubble sort (bubble sort): Correct and common.

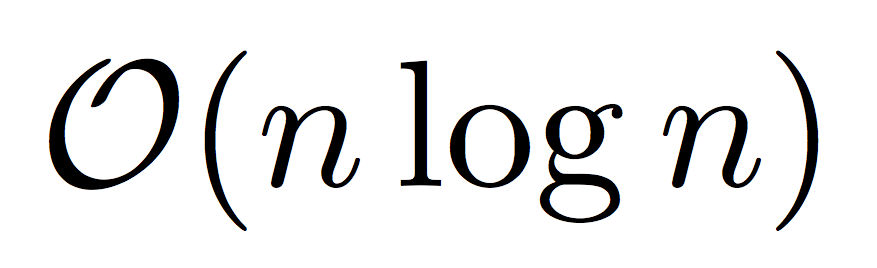





[…] Binary search gets much faster as n gets larger. In computer science fundamentals, these concepts (Big O notation) are covered in later lessons […]