Quick Sort Guide: Divide and Conquer Algorithm

Sorting is a cornerstone of computer science. It's found everywhere, from databases to search algorithms. Among the many sorting algorithms Quick Sort Quick Sort is both fast and widely used. Developed by Tony Hoare in 1960, this algorithm stands out for its "divide and conquer" approach. In this guide, we'll explore how Quick Sort works, its time complexity, and how it's implemented in different programming languages. I'll explain this algorithm with examples from my own projects. If you're ready, let's get started!

How Does Quick Sort Work?

Quick Sort operates efficiently using a "divide and conquer" strategy. In Turkish, "Quick Sort" is used similarly to its English name and is well-established in the literature. The basic idea is to select a pivot element from the array and divide the other elements into two sub-arrays relative to the pivot: those smaller than the pivot and those larger. These sub-arrays are then sorted recursively.

Let's explain it step by step:

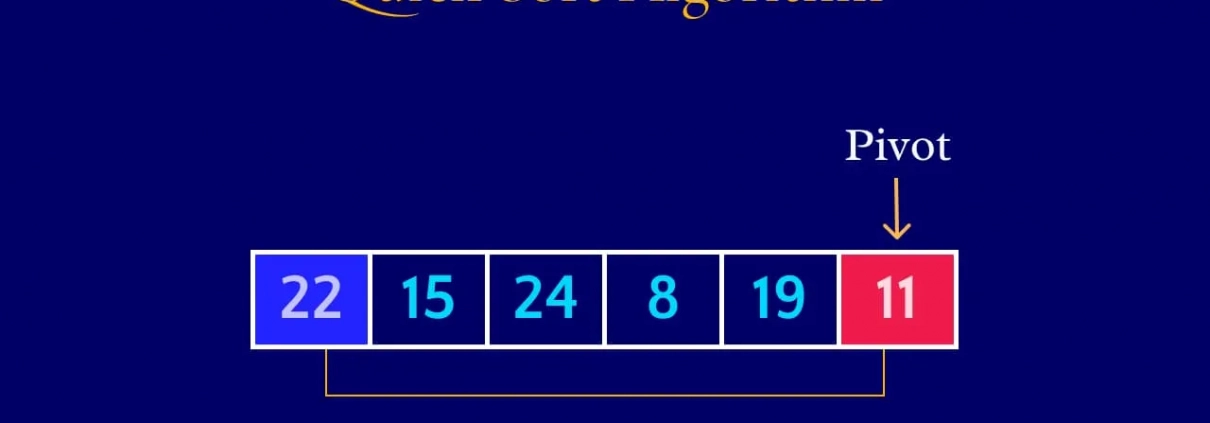
1. Pivot Selection: A pivot element is selected from the array. The pivot selection affects the performance of the algorithm (we will examine this in detail later).
2. Splitting the ArrayElements smaller than the pivot are placed to the left, and elements larger than the pivot are placed to the right. The pivot is then placed in its final sequential position. In Turkish, this process is called "partitioning."
3. Sorting Substrings: The left and right sub-arrays are sorted recursively with Quick Sort.
4. Merge: Since the substrings are sorted, when concatenated the entire string becomes sorted.

An example with Python:

def quicksort(array): if len(array) <= 1: return array # Base case: Array with 0 or 1 elements is already sorted pivot = array[len(array) // 2] # Select the middle element as the pivot left = [x for x in array if x < pivot] middle = [x for x in array if x == pivot] right = [x for x in array if x > pivot] return quicksort(left) + middle + quicksort(right) # Sort left and right subarrays # Example usage array = [3, 6, 8, 10, 1, 2, 1] print("Sorted Array:", quicksort(array)) # Output: [1, 1, 2, 3, 6, 8, 10]

Time Complexity of Quick Sort

Quick Sort has impressive performance in the average case. Average and best case time complexity O(n log n), where "n" is the number of elements in the array. However, if poorly chosen pivots split the array unevenly, the worst-case complexity O(n²) it could be.

In a data analysis project, I sorted a large dataset using Quick Sort, and its performance was great in the average case. However, I experienced a few slowdowns due to poor pivot selection. This is why pivot selection is so important!

Pivot Selection Strategies

Pivot selection directly impacts Quick Sort's performance. Here are some strategies:

• Random Pivot: Choosing a random element helps prevent the worst case scenario.
• Triple Median Pivot: Choosing the median of the first, middle, and last elements of the array balances the subarrays.
• Advanced Pivot SelectionMethods like Introselect intelligently choose pivots based on the data structure.

Quick Sorting in Different Programming Languages

Quick Sort can be easily implemented in different languages. Here are examples from JavaScript and C++:

JavaScript

function hizliSiralama(dizi) {
if (dizi.length <= 1) {
return dizi;
}

const pivot = dizi[Math.floor(dizi.length / 2)];
const sol = dizi.filter(eleman => eleman < pivot);
const orta = dizi.filter(eleman => eleman === pivot);
const sag = dizi.filter(eleman => eleman > pivot);

return [...hizliSiralama(sol), ...orta, ...hizliSiralama(sag)];
}

// Örnek kullanım
const dizi = [3, 6, 8, 10, 1, 2, 1];
console.log(hizliSiralama(dizi)); // Çıktı: [1, 1, 2, 3, 6, 8, 10]

C++

#include #include std::vector quickSort(std::vector array) { if (array.size() <= 1) { return array; } int pivot = array[array.size() / 2]; std::vector left, middle, right; for (int element : array) { if (element < pivot) { sol.push_back(element); } else if (element == pivot) { middle.push_back(element); } else { sag.push_back(element); } } left = quickSort(left); right = quickSort(right); sol.insert(sol.end(), middle.begin(), middle.end()); left.insert(left.end(), right.begin(), right.end()); return left; } int main() { std::vector array = {3, 6, 8, 10, 1, 2, 1}; std::vector sortedArray = quickSort(array); for (int element : sortedArray) { std::cout << element << " "; } return 0; }

Conclusion

QuickSort is a fast and efficient sorting algorithm with a divide-and-conquer strategy. Its average complexity of O(n log n) makes it ideal for large datasets. Optimizations around pivot selection prevent the worst-case scenario. In one sorting project, I used QuickSort to sort millions of datasets in seconds, and the results were fantastic!

Which projects have you used Quick Sort on? Have you discovered a trick for pivot selection? Share it in the comments, and let's discuss it together! For more algorithm tips, check out my blog or contact me!

Notes

• Turkish Equivalents of Terms:
  • Quick Sort (Quick Sort): Established, correct and widespread in Turkish.
  • Divide and conquer (divide and conquer): Standard in the algorithm literature.
  • Pivot: It is used exactly as in Turkish, it is a common term.
  • Divide (partitioning): A correct and established response.