The Infinite Monkey Theorem (or, On the Power of Coincidences)
The concept of the 'Infinite Monkey Theorem' can be translated as 'an infinite number of monkeys theorem' or 'a monkey theorem with infinite time.' This theorem has nothing to do with evolution, as some might think. It is a theorem that addresses the formation of the universe. It demonstrates that the formation of the universe can be attributed entirely to chance, and that if the probability of that chance is positive (i.e., not impossible), then no matter how low the probability, that coincidence will eventually occur.
 Let's explain the theorem like this: Place a monkey in front of a typewriter and press the keys. Let's say the typewriter has fifty keys, including letters. Because the monkey doesn't know what it's doing or why, the first time it presses a key, the probability of hitting the letter "b" is one in fifty. The probability of typing something long and meaningful like "big bang" is much, much smaller; the probability will decrease by "fiftieths of one-fiftieth ...
Let's explain the theorem like this: Place a monkey in front of a typewriter and press the keys. Let's say the typewriter has fifty keys, including letters. Because the monkey doesn't know what it's doing or why, the first time it presses a key, the probability of hitting the letter "b" is one in fifty. The probability of typing something long and meaningful like "big bang" is much, much smaller; the probability will decrease by "fiftieths of one-fiftieth ...
The point I'm trying to make is this: We can apply the same considerations to the Big Bang itself as we do to the probability of a monkey accidentally typing the "Big Bang" sequence into a typewriter! The probability of the Big Bang creating our universe is extremely small, but it's not zero. How do we know it's not zero? By seeing that we're inside the universe. So how do we know it's a very low probability? When we look at the balances and physical properties within the universe, we see that these balances must have come together through a tremendous coincidence. Some people are putting forward the "creator" thesis here, and at first glance, they're right. But we'll take a second look here!
What we said: The probability of the universe's formation is very low. Perhaps this probability is as low as the probability of that monkey accidentally typing letters into a typewriter and accidentally typing a novel like "The Lord of the Rings," and perhaps even lower. But if you had the option to wait long enough, you would have witnessed the monkey writing that novel. So, even if the probability of the universe's formation is so small that it's beyond our comprehension, the probability of it being greater than zero will inevitably occur if you wait forever! To give you another example that might make more sense: If you participate in every National Lottery drawing, and if there's no fraud, your chances of winning the highest jackpot in one of these drawings, if you live long enough, will gradually approach infinity, approaching absolute probability. In other words, the longer you play, the more certain you become of eventually winning the highest jackpot. Even if the odds of winning a single game remain constant at a vanishingly small probability, unchanging.
How meaningful is it to speak of "eternity" before the Big Bang, where time hadn't yet formed? Time as we know it doesn't pass during or before the Big Bang. So, even if the probability of any crazy thought you have is very low, if it's greater than zero, it will definitely happen, because that crazy event has an eternity of time, with no time passing. And that's not all: Events with a probability greater than zero will not occur just once, but an infinite number of times, because the probability of these events will not change once they occur.
Finally, we must remember that many seemingly miraculous physical phenomena may appear so simply because they lack explanations at the current state of science. There are numerous examples of this in the history of science. But science doesn't stand still. Ultimately, future theories may make these precise values seem perfectly normal. Even if they aren't, the point I made above remains true. We are continuing to study these phenomena and will continue to open closed doors. Be assured of this!
Author: İlker Savas





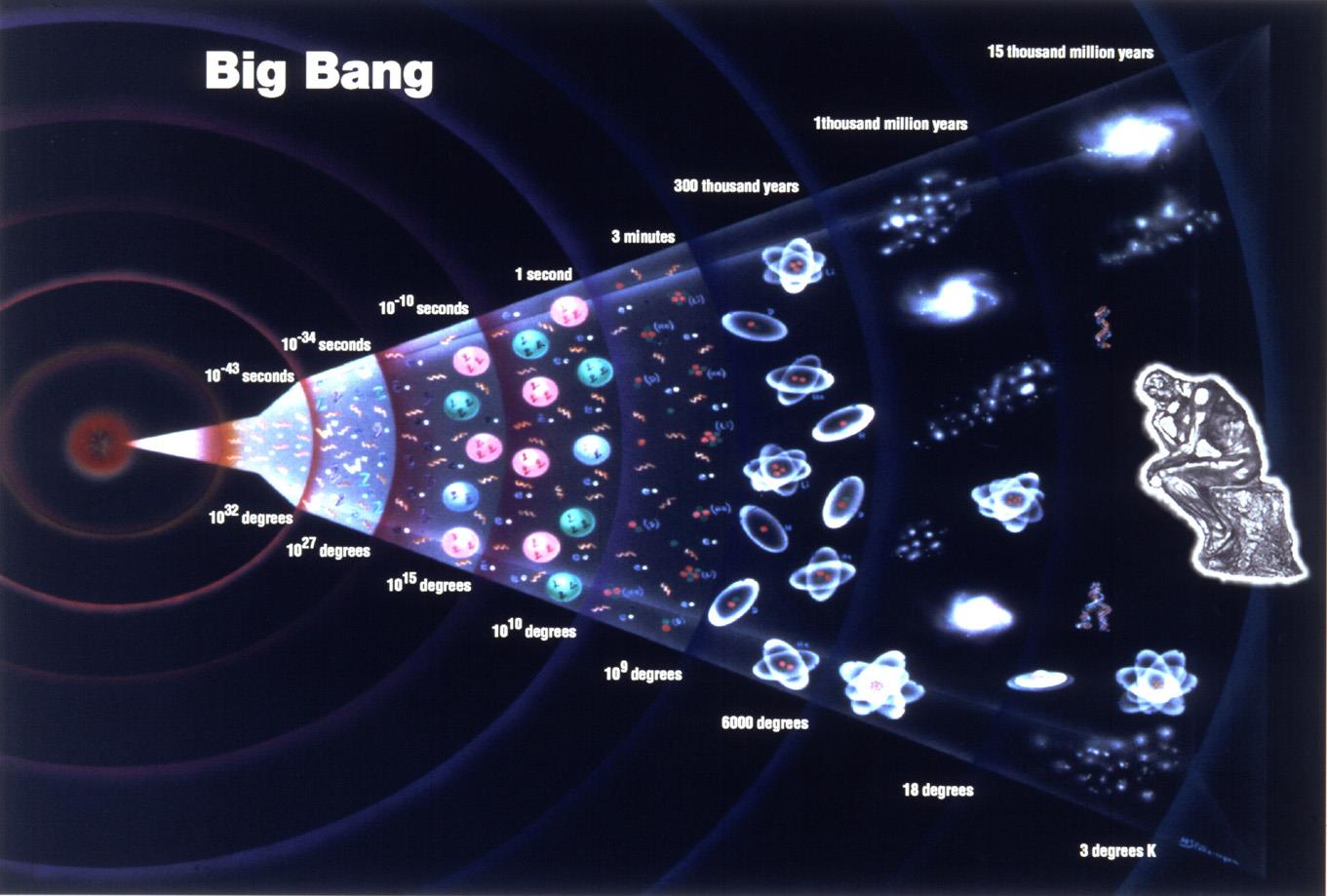



However, there's a problem with this Infinite Monkey Theory: "Infinite Time." How does this monkey find infinite time? Or how can the Big Bang explode infinitely many times?