
Dijkstra Algoritması: Python ile Pratik Rehber
0 Yorumlar
/
Dijkstra Algoritması, 1956’da Hollandalı bilgisayar bilimci…

Birleştirme Sıralaması ve Hızlı Sıralama Rehberi: Böl ve Fethet Algoritmaları
Sıralama, bilgisayar bilimlerinin temel taşlarından biridir…

İkili Arama Algoritması: Verimlilik
Arama, bilgisayar bilimlerinin temel işlemlerinden biridir ve…
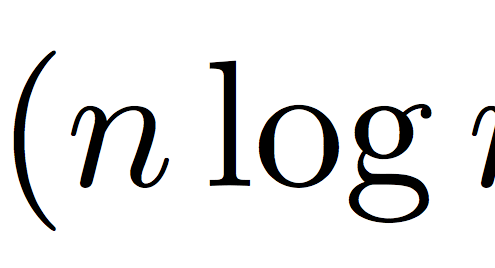
Büyük O Notasyonu Rehberi: Algoritma Verimliliğini Anlama
Algoritmaların verimliliği, bilgisayar bilimleri ve programlama…

Kabarcık Sıralaması Algoritması: Sıralamanın Basitliği
Kabarcık Sıralaması Algoritması: Sıralamanın…

Algoritma: Mantık ve Verimlilik Yolculuğu
Modern teknolojinin karmaşık dokusunda, algoritmalar…
