Derinlik Öncelikli Arama (DFS) Algoritması Rehberi

Graf teorisi ve algoritmalar dünyasında, Derinlik Öncelikli Arama (DFS, Depth-First Search) temel ve çok yönlü bir araçtır. Graf veri yapılarını keşfetmek ve taramak için kullanılan bu algoritma, yol bulma, döngü tespiti, topolojik sıralama gibi birçok alanda vazgeçilmezdir. Bu rehberde, DFS’nin temellerini, uygulamalarını ve Python ile pratik örneklerini derinlemesine inceleyeceğiz. Kendi deneyimlerimden örneklerle, bu algoritmayı sizin için anlaşılır hale getireceğim. Hazırsanız, başlayalım!

Derinlik Öncelikli Arama Nedir?

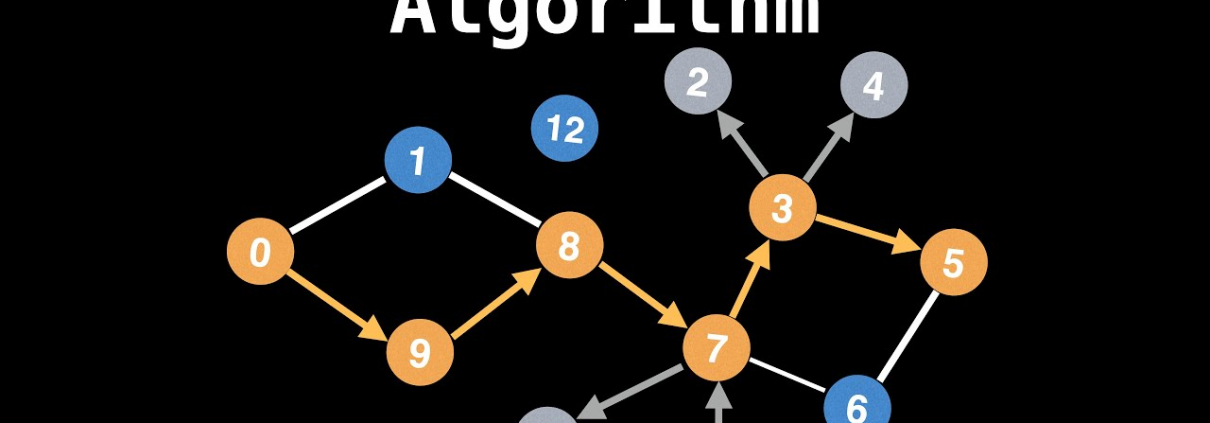
DFS, bir grafın dallarını mümkün olduğunca derinlemesine keşfeden bir tarama algoritmasıdır. Türkçe’de “derinlik öncelikli arama” terimi, İngilizce’deki “Depth-First Search” için doğrudan kullanılır ve literatürde yerleşmiştir. Bir dalı sonuna kadar keşfettikten sonra geri dönerek diğer dalları inceler. Temel fikir, düğümleri sistematik olarak ziyaret etmek, ziyaret edilenleri işaretlemek ve ziyaret edilmemiş komşuları rekürsif olarak keşfetmektir.

DFS’nin Temel Bileşenleri

DFS’yi anlamak için temel bileşenlere bakalım:

• Yığın (veya Rekürsiyon): Ziyaret edilecek düğümleri takip etmek için bir yığın kullanılır. Rekürsiyon, yığının davranışını doğal olarak taklit eder. Türkçe’de “yığın” (stack) standart bir terim.
• Ziyaret Edilenler Kümesi: Tekrar ziyaretleri önlemek için düğümler bir küme veya dizi ile işaretlenir.
• Graf Temsili: Graf, genellikle komşuluk listesi veya komşuluk matrisi ile temsil edilir. Türkçe’de bu terimler (adjacency list/matrix) aynen kullanılır.

DFS Algoritmasının Adımları

DFS, şu adımları takip eder:

1. Başlangıç düğümünden başlayın ve onu ziyaret edilmiş olarak işaretleyin.
2. Mevcut düğümün ziyaret edilmemiş bir komşusunu seçin.
3. Komşu varsa, onu yığına ekleyin (veya rekürsif çağırın) ve 2. adıma dönün.
4. Komşu yoksa, bir önceki düğüme geri dönün (yığından çıkarın veya rekürsiyonu sonlandırın).
5. Yığın boşalana kadar 2-4. adımları tekrarlayın.

DFS’nin Uygulamaları

DFS, bilgisayar bilimlerinde birçok alanda kullanılır:

• Yol Bulma: Graf içindeki iki düğüm arasındaki yolları bulur (örneğin, bir haritada rota bulma).
• Döngü Tespiti: Grafta döngü olup olmadığını kontrol eder (örneğin, işletim sistemlerinde kilitlenme tespiti).
• Topolojik Sıralama: Yönlendirilmiş döngüsüz graflarda (DAG) sıralama yapar (örneğin, görev zamanlama).
• Bağlantılı Bileşenler: Grafın bağlantılı parçalarını belirler.
• Ağaç Taraması: Ağaçlarda (grafın özel bir türü) öncelikli, sıralı veya sonradan sıralı tarama yapar.

Bir keresinde, bir sosyal ağ analizinde DFS kullanarak kullanıcı gruplarını (bağlantılı bileşenleri) tespit ettim ve bu, veri analizini çok kolaylaştırdı!

Python ile DFS Örnekleri

Komşuluk Listesi ile DFS

Bir grafı komşuluk listesiyle temsil edelim ve DFS’yi yığın kullanarak uygulayalım:

def dfs(graf, baslangic):
ziyaret_edilen = set()
yigin = [baslangic]

while yigin:
dugum = yigin.pop()
if dugum not in ziyaret_edilen:
print(dugum, end=' ') # Düğümü işle (isteğe göre değiştir)
ziyaret_edilen.add(dugum)
yigin.extend(komsu for komsu in graf[dugum] if komsu not in ziyaret_edilen)

# Örnek kullanım
graf = {
0: [1, 2],
1: [0, 3, 4],
2: [0, 4],
3: [1],
4: [1, 2]
}
dfs(graf, 0) # Çıktı: 0 2 4 1 3

Bu kodda:

• Başlangıç düğümünü yığına ekliyoruz.
• Yığından bir düğüm alıp ziyaret ediyoruz, komşularını yığına ekliyoruz.
• Yığın boşalana kadar devam ediyoruz.

Komşuluk Matrisi ile DFS

Graf bir komşuluk matrisiyle temsil edildiğinde:

def dfs_matris(matris, baslangic):
n = len(matris)
ziyaret_edilen = set()
yigin = [baslangic]

while yigin:
dugum = yigin.pop()
if dugum not in ziyaret_edilen:
print(dugum, end=' ') # Düğümü işle (isteğe göre değiştir)
ziyaret_edilen.add(dugum)
komsular = [i for i in range(n) if matris[dugum][i] == 1 and i not in ziyaret_edilen]
yigin.extend(komsular)

# Örnek kullanım
matris = [
[0, 1, 1, 0, 0],
[1, 0, 0, 1, 1],
[1, 0, 0, 0, 1],
[0, 1, 0, 0, 0],
[0, 1, 1, 0, 0]
]
dfs_matris(matris, 0) # Çıktı: 0 2 4 1 3

Bu kodda, matrisin 1’leri kenarları temsil eder. DFS, komşuları bulur ve yığınla taramayı sürdürür.

Sonuç

Derinlik Öncelikli Arama (DFS), grafları sistematik bir şekilde keşfetmek için güçlü bir algoritmadır. Yol bulma, döngü tespiti veya topolojik sıralama gibi birçok alanda kullanılır. Bu rehberdeki örneklerle, DFS’nin nasıl çalıştığını ve projelerinizde nasıl uygulayacağınızı öğrendiniz. Bir labirent çözüm projesinde DFS kullanarak en kısa yolu buldum ve sonuçlar hem hızlı hem de etkileyiciydi!

Siz DFS ile hangi problemleri çözdünüz? İlginç bir deneyiminiz mi var? Yorumlarda paylaşın, birlikte tartışalım! Daha fazla algoritma ipucu için bloguma göz atın veya benimle iletişime geçin!

Notlar

• Terimlerin Türkçe Karşılıkları:
  • Derinlik Öncelikli Arama (Depth-First Search): Türkçede yerleşmiş, doğru ve yaygın.
  • Yığın (stack), komşuluk listesi (adjacency list), komşuluk matrisi (adjacency matrix): Makine öğrenimi ve algoritma literatüründe standart.
  • Ziyaret edilenler kümesi (visited set): Doğru ve yaygın.
  • Topolojik sıralama (topological sorting): Standart terim.