Büyük O Notasyonu Rehberi: Algoritma Verimliliğini Anlama
Algoritmaların verimliliği, bilgisayar bilimleri ve programlama dünyasında kritik bir öneme sahip. Aynı problemi çözen iki farklı yöntem düşünün; ikisi de doğru sonucu verebilir, ama biri diğerinden çok daha yavaş olabilir. İşte burada Büyük O Notasyonu devreye giriyor. Algoritmaların performansını ölçmek ve karşılaştırmak için kullanılan bu araç, verimli çözümler tasarlamada rehberimiz. Bu yazıda, Büyük O Notasyonu’nun ne olduğunu, neden önemli olduğunu ve nasıl yorumlanacağını keşfedeceğiz. Kendi deneyimlerimden örneklerle, bu kavramı sizin için anlaşılır hale getireceğim. Hazırsanız, başlayalım!
Temel: Büyük O Notasyonu Nedir?
Büyük O Notasyonu, bir algoritmanın performansını veya zaman karmaşıklığını matematiksel olarak tanımlamanın bir yoludur. Türkçe’de “Büyük O Notasyonu” (Big O Notation) terimi, İngilizce adıyla aynı şekilde kullanılır ve literatürde yerleşmiştir. Algoritmanın çalışma süresinin, giriş verisi büyüklüğüne (n) bağlı olarak nasıl değiştiğini gösterir. Basitçe, şu soruya yanıt verir: “Giriş verisi büyüdükçe algoritmanın çalışma süresi nasıl artar?”
Örnek olarak, bir dizide eleman aramayı ele alalım. Doğrusal Arama (Linear Search), diziyi tek tek tarar ve hedef elemanı bulana kadar devam eder. Bu algoritma, O(n) zaman karmaşıklığına sahiptir; burada “n” dizinin eleman sayısıdır.
def dogrusal_arama(dizi, hedef):
for eleman in dizi:
if eleman == hedef:
return True
return FalseAncak her algoritma doğrusal çalışmaz. Büyük O Notasyonu, algoritmaları giriş büyüklüğüne bağlı olarak sınıflandırmamızı sağlar ve hangi algoritmanın daha verimli olduğunu anlamamıza yardımcı olur.
Notasyon: Sembolleri Çözümleme
Büyük O Notasyonu, ilk bakışta korkutucu görünebilen semboller ve terimlerle ifade edilir. En yaygın olanları inceleyelim:
1. O(1) – Sabit Zaman Karmaşıklığı
Sabit zamanlı algoritmalar, giriş büyüklüğünden bağımsız olarak aynı sürede çalışır. Örneğin, bir diziden indeksiyle eleman çekmek:
def eleman_erişim(dizi, indeks):
return dizi[indeks]Dizi 10 elemanlı da olsa 1.000 elemanlı da, bu işlem sabit sürede tamamlanır.
2. O(log n) – Logaritmik Zaman Karmaşıklığı
Logaritmik algoritmalar, her adımda giriş verisini yarıya indirir. İkili Arama (Binary Search) bunun klasik örneğidir. Giriş büyüdükçe, adım sayısı logaritmik olarak artar.
def ikili_arama(dizi, hedef):
sol, sag = 0, len(dizi) - 1
while sol <= sag:
orta = (sol + sag) // 2
if dizi[orta] == hedef:
return orta
elif dizi[orta] < hedef:
sol = orta + 1
else:
sag = orta - 1
return -1Bir veri tabanı projesinde, İkili Arama kullanarak sıralı bir listede hızlıca arama yaptım ve sonuçlar inanılmaz hızlıydı!
3. O(n) – Doğrusal Zaman Karmaşıklığı
Doğrusal algoritmalar, giriş büyüklüğüyle orantılı olarak çalışır. Örneğin, bir dizinin toplamını hesaplamak:
def dogrusal_toplama(dizi):
toplam = 0
for eleman in dizi:
toplam += eleman
return toplamGiriş büyüklüğü iki katına çıkarsa, çalışma süresi de yaklaşık iki katına çıkar.
4. O(n log n) – Lineer-Logaritmik Zaman Karmaşıklığı
Birleştirme Sıralaması (Merge Sort) ve Hızlı Sıralama (Quick Sort) gibi algoritmalar bu kategoriye girer. Doğrusal algoritmalardan biraz daha yavaş, ama karesel algoritmalardan çok daha hızlıdır.
def birlestirme_siralamasi(dizi):
if len(dizi) <= 1:
return dizi
orta = len(dizi) // 2
sol_yari = dizi[:orta]
sag_yari = dizi[orta:]
sol_yari = birlestirme_siralamasi(sol_yari)
sag_yari = birlestirme_siralamasi(sag_yari)
return birlestir(sol_yari, sag_yari)
def birlestir(sol, sag):
sonuc = []
sol_indeks, sag_indeks = 0, 0
while sol_indeks < len(sol) and sag_indeks < len(sag):
if sol[sol_indeks] < sag[sag_indeks]:
sonuc.append(sol[sol_indeks])
sol_indeks += 1
else:
sonuc.append(sag[sag_indeks])
sag_indeks += 1
sonuc.extend(sol[sol_indeks:])
sonuc.extend(sag[sag_indeks:])
return sonuc5. O(n²) – Karesel Zaman Karmaşıklığı
Karesel algoritmalar, giriş büyüklüğünün karesiyle orantılı çalışır. Örneğin, Kabarcık Sıralaması (Bubble Sort):
def kabarcik_siralamasi(dizi):
n = len(dizi)
for i in range(n):
for j in range(0, n - i - 1):
if dizi[j] > dizi[j + 1]:
dizi[j], dizi[j + 1] = dizi[j + 1], dizi[j]Giriş büyüklüğü iki katına çıkarsa, çalışma süresi dört katına çıkar. Küçük veri setlerinde sorun olmasa da, büyük veri setlerinde yavaş olabilir.
6. O(2^n) – Üstel Zaman Karmaşıklığı
Üstel algoritmalar, giriş büyüklüğüyle üssel olarak büyür. Örneğin, rekürsif Fibonacci hesaplama:
def fibonacci_rekursif(n):
if n <= 1:
return n
return fibonacci_rekursif(n - 1) + fibonacci_rekursif(n - 2)Bu tür algoritmalar, büyük girişlerde yönetilemez hale gelir.
7. O(n!) – Faktöriyel Zaman Karmaşıklığı
En yavaş algoritmalar, faktöriyel hızda büyür. Örneğin, tüm permütasyonları oluşturma:
def permutasyon_olustur(elemanlar):
if len(elemanlar) == 1:
return [elemanlar]
permutasyonlar = []
for i, eleman in enumerate(elemanlar):
kalan_elemanlar = elemanlar[:i] + elemanlar[i+1:]
for perm in permutasyon_olustur(kalan_elemanlar):
permutasyonlar.append([eleman] + perm)
return permutasyonlarBu algoritmalar, genellikle kaçınılması gereken kadar yavaştır.
Gerçek Hayatta Büyük O Notasyonu
Büyük O Notasyonu, sadece teorik bir araç değil, pratik kararlar için de kritik. Bir sıralama problemi için algoritma seçerken, Büyük O Notasyonu size rehberlik eder. Örneğin, küçük bir dizide karesel bir algoritma hızlı olabilir, ama büyük veri setlerinde O(n log n) algoritmalar fark yaratır. Bir e-ticaret projesinde, büyük bir ürün listesini sıralamak için Birleştirme Sıralaması’nı seçtim ve performans harikaydı!
Gizli Faktörler: Alan Karmaşıklığı ve Gerçek Dünya
Büyük O Notasyonu, genellikle zaman karmaşıklığına odaklanır, ama alan karmaşıklığı da önemlidir. Türkçe’de “alan karmaşıklığı” (space complexity) standart bir terim. Bazı algoritmalar, sınırlı bellekli cihazlarda sorun yaratabilir. Ayrıca, programlama dili, donanım mimarisi ve sabit faktörler gibi gerçek dünya koşulları, algoritma seçimini etkiler. Büyük O, genel bir bakış sunar, ama mutlak bir garanti değildir.
Sonuç
Büyük O Notasyonu, algoritmaların verimliliğini analiz etmek ve karşılaştırmak için güçlü bir araçtır. Algoritmaları giriş büyüklüğüne göre sınıflandırmayı sağlar ve programcılara bilinçli kararlar alma gücü verir. Ancak, gerçek dünya koşulları ve pratik kısıtlamalar da dikkate alınmalı. Bir veri analizi projesinde, Büyük O Notasyonu sayesinde doğru algoritmayı seçerek performansı optimize ettim. Siz de bu notasyonu rehber edin, verimli çözümler tasarlayın!
Siz Büyük O Notasyonu’nu hangi projelerde kullandınız? İlginç bir deneyim mi yaşadınız? Yorumlarda paylaşın, birlikte tartışalım! Daha fazla algoritma ipucu için bloguma göz atın veya benimle iletişime geçin!
Notlar
- Terimlerin Türkçe Karşılıkları:
- Büyük O Notasyonu (Big O Notation): Türkçede yerleşmiş, doğru ve yaygın.
- Zaman karmaşıklığı (time complexity), alan karmaşıklığı (space complexity): Algoritma literatüründe standart.
- Doğrusal arama (linear search), ikili arama (binary search), kabarcık sıralaması (bubble sort): Doğru ve yaygın.

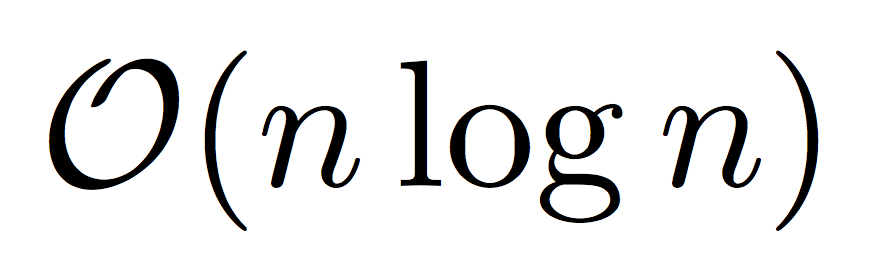





[…] n büyüdükçe ikili arama çok daha hızlıdır. Bilgisayar bilimi temellerinde, bu kavramlar (Big O notasyonu) ilerleyen derslerde […]