Hızlı Sıralama (Quick Sort) Rehberi: Böl ve Fethet Algoritması
Sıralama, bilgisayar bilimlerinin temel taşlarından biri. Veritabanlarından arama algoritmalarına kadar her yerde karşımıza çıkıyor. Birçok sıralama algoritması arasında Hızlı Sıralama (Quick Sort), hem hızlı hem de yaygın kullanılan bir yöntem. 1960’ta Tony Hoare tarafından geliştirilen bu algoritma, “böl ve fethet” yaklaşımıyla öne çıkıyor. Bu rehberde, Hızlı Sıralama’nın nasıl çalıştığını, zaman karmaşıklığını ve farklı programlama dillerinde nasıl uygulandığını keşfedeceğiz. Kendi projelerimden örneklerle, bu algoritmayı sizin için anlaşılır hale getireceğim. Hazırsanız, başlayalım!
Hızlı Sıralama Nasıl Çalışır?
Hızlı Sıralama, “böl ve fethet” stratejisiyle verimli bir şekilde çalışır. Türkçe’de “Hızlı Sıralama” (Quick Sort), İngilizce adıyla aynı şekilde kullanılır ve literatürde yerleşmiştir. Temel fikir, diziden bir “pivot” eleman seçmek ve diğer elemanları pivot’a göre iki alt diziye ayırmaktır: pivot’tan küçük olanlar ve büyük olanlar. Ardından bu alt diziler rekürsif olarak sıralanır.
Adım adım açıklayalım:
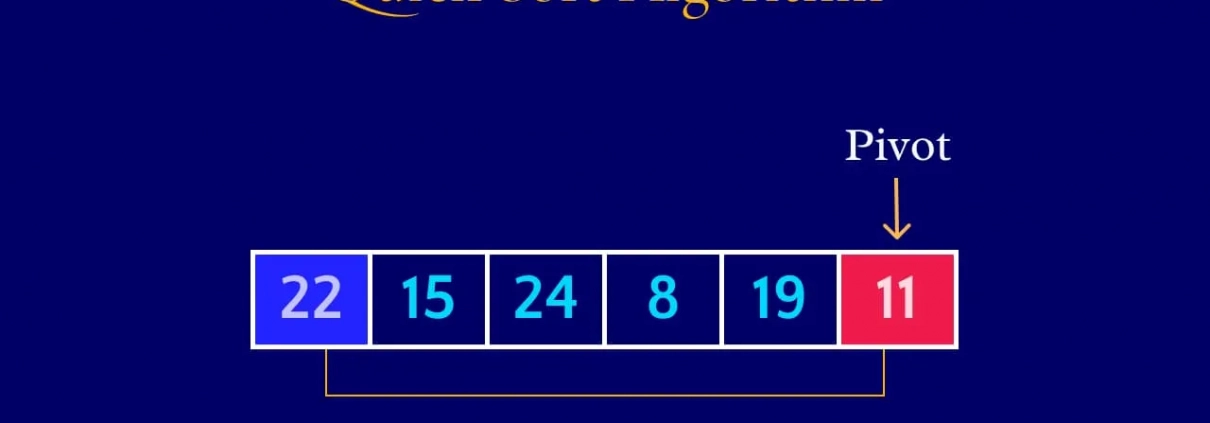
- Pivot Seçimi: Diziden bir pivot eleman seçilir. Pivot seçimi, algoritmanın performansını etkiler (bunu ileride detaylı inceleyeceğiz).
- Diziyi Bölme: Elemanlar, pivot’tan küçük olanlar sola, büyük olanlar sağa yerleştirilir. Pivot, nihai sıralı konumuna yerleşir. Türkçe’de bu işleme “bölme” (partitioning) denir.
- Alt Dizileri Sıralama: Sol ve sağ alt diziler, rekürsif olarak Hızlı Sıralama ile sıralanır.
- Birleştirme: Alt diziler sıralı olduğu için, birleştirildiğinde tüm dizi sıralanmış olur.
Python ile bir örnek:
def hizli_siralama(dizi):
if len(dizi) <= 1:
return dizi # Temel durum: 0 veya 1 elemanlı dizi zaten sıralıdır
pivot = dizi[len(dizi) // 2] # Ortadaki elemanı pivot olarak seç
sol = [x for x in dizi if x < pivot]
orta = [x for x in dizi if x == pivot]
sag = [x for x in dizi if x > pivot]
return hizli_siralama(sol) + orta + hizli_siralama(sag) # Sol ve sağ alt dizileri sırala
# Örnek kullanım
dizi = [3, 6, 8, 10, 1, 2, 1]
print("Sıralanmış Dizi:", hizli_siralama(dizi)) # Çıktı: [1, 1, 2, 3, 6, 8, 10]
Hızlı Sıralama’nın Zaman Karmaşıklığı
Hızlı Sıralama, ortalama durumda etkileyici bir performansa sahip. Ortalama ve en iyi durumda zaman karmaşıklığı O(n log n), burada “n” dizideki eleman sayısı. Ancak, kötü seçilmiş pivotlar diziyi dengesiz bölerse, en kötü durumda karmaşıklık O(n²) olabilir.
Bir veri analizi projesinde, Hızlı Sıralama kullanarak büyük bir veri setini sıraladım ve ortalama durumda performansı harikaydı. Ama kötü pivot seçiminden dolayı birkaç kez yavaşlama yaşadım. Bu yüzden pivot seçimi çok önemli!
Pivot Seçimi Stratejileri
Pivot seçimi, Hızlı Sıralama’nın performansını doğrudan etkiler. İşte bazı stratejiler:
- Rastgele Pivot: Rastgele bir eleman seçmek, en kötü durumu önlemeye yardımcı olur.
- Üçlü Medyan Pivot: Dizinin ilk, orta ve son elemanlarının medyanını seçmek, alt dizileri dengeler.
- Gelişmiş Pivot Seçimi: Introselect gibi yöntemler, veri yapısına göre akıllıca pivot seçer.
Farklı Programlama Dillerinde Hızlı Sıralama
Hızlı Sıralama, farklı dillerde kolayca uygulanabilir. İşte JavaScript ve C++ örnekleri:
JavaScript
function hizliSiralama(dizi) {
if (dizi.length <= 1) {
return dizi;
}
const pivot = dizi[Math.floor(dizi.length / 2)];
const sol = dizi.filter(eleman => eleman < pivot);
const orta = dizi.filter(eleman => eleman === pivot);
const sag = dizi.filter(eleman => eleman > pivot);
return [...hizliSiralama(sol), ...orta, ...hizliSiralama(sag)];
}
// Örnek kullanım
const dizi = [3, 6, 8, 10, 1, 2, 1];
console.log(hizliSiralama(dizi)); // Çıktı: [1, 1, 2, 3, 6, 8, 10]
C++
#include <iostream>
#include <vector>
std::vector<int> hizliSiralama(std::vector<int> dizi) {
if (dizi.size() <= 1) {
return dizi;
}
int pivot = dizi[dizi.size() / 2];
std::vector<int> sol, orta, sag;
for (int eleman : dizi) {
if (eleman < pivot) {
sol.push_back(eleman);
} else if (eleman == pivot) {
orta.push_back(eleman);
} else {
sag.push_back(eleman);
}
}
sol = hizliSiralama(sol);
sag = hizliSiralama(sag);
sol.insert(sol.end(), orta.begin(), orta.end());
sol.insert(sol.end(), sag.begin(), sag.end());
return sol;
}
int main() {
std::vector<int> dizi = {3, 6, 8, 10, 1, 2, 1};
std::vector<int> siralanmisDizi = hizliSiralama(dizi);
for (int eleman : siralanmisDizi) {
std::cout << eleman << " ";
}
return 0;
}
Sonuç
Hızlı Sıralama, böl ve fethet stratejisiyle hızlı ve etkili bir sıralama algoritmasıdır. Ortalama durumda O(n log n) karmaşıklığı, onu büyük veri setleri için ideal yapar. Pivot seçimiyle ilgili optimizasyonlar, en kötü durumları önler. Bir sıralama projesinde Hızlı Sıralama kullanarak milyonlarca veriyi saniyeler içinde sıraladım ve sonuçlar harikaydı!
Siz Hızlı Sıralama’yı hangi projelerde kullandınız? Pivot seçimiyle ilgili bir püf noktası mı keşfettiniz? Yorumlarda paylaşın, birlikte tartışalım! Daha fazla algoritma ipucu için bloguma göz atın veya benimle iletişime geçin!
Notlar
- Terimlerin Türkçe Karşılıkları:
- Hızlı Sıralama (Quick Sort): Türkçede yerleşmiş, doğru ve yaygın.
- Böl ve fethet (divide and conquer): Algoritma literatüründe standart.
- Pivot: Türkçe’de aynen kullanılır, yaygın bir terim.
- Bölme (partitioning): Doğru ve yerleşmiş bir karşılık.