Mastering Decision Trees: A Guide with Practical Python Examples

Decision trees are a fundamental machine-learning technique used for both classification and regression tasks. They are intuitive, and interpretable, and can be valuable tools in various domains, from finance to healthcare and beyond. In this guide, you will explore decision trees in detail, including their principles, construction, evaluation, and practical implementation with code examples in Python.

Introduction to Decision Trees
Anatomy of a Decision Tree
Decision Tree Construction
– Entropy and Information Gain
– Gini Impurity
Decision Tree Algorithms
– ID3
– C4.5 (C5.0)
– CART
Decision Tree Pruning
Decision Tree in Practice
– Data Preparation
– Decision Tree in Python
– Decision Tree Visualization
Evaluation of Decision Trees
– Confusion Matrix
– Cross-Validation
– Overfitting
Advantages and Disadvantages
Conclusion

1. Introduction to Decision Trees

A decision tree is a supervised machine learning algorithm that makes predictions by learning a hierarchy of if-else questions. It mimics the way humans make decisions by breaking down complex problems into a series of simpler decisions. Each node in the tree represents a decision, and each branch represents an outcome of that decision.

Decision trees are used in various applications, including:

Classification: Assigning an object to one of several predefined classes.
Regression: Predicting a continuous numeric value.

2. Anatomy of a Decision Tree

A typical decision tree consists of three main elements:

Root Node: The topmost node, which represents the initial decision.
Internal Nodes: Intermediate nodes that represent decisions.
Leaf Nodes: Terminal nodes that provide the final output or prediction.

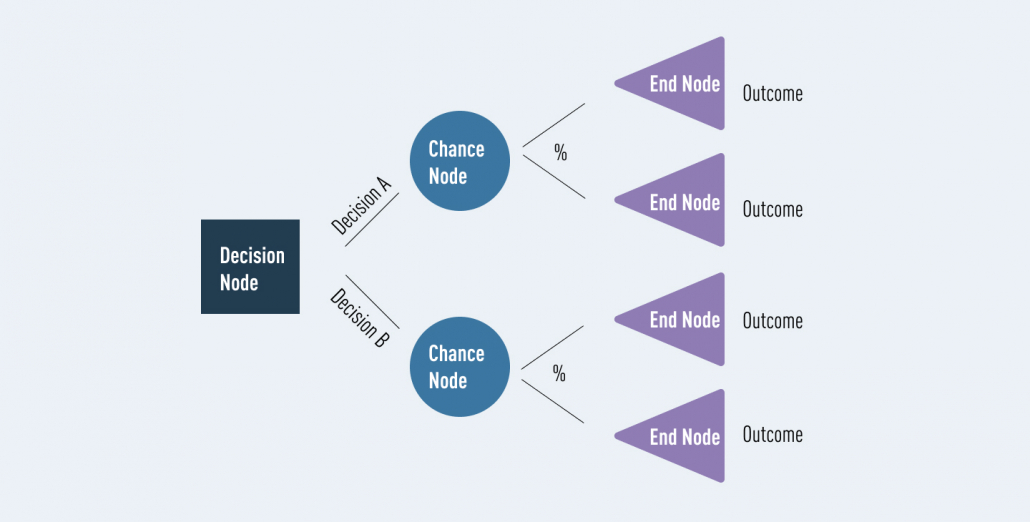
Decision Tree Anatomy

3. Decision Tree Construction

Decision trees are constructed using a recursive process that selects the best feature to split the data at each node. Two popular metrics used for this purpose are Entropy and Gini impurity.

Entropy and Information Gain

Entropy measures the randomness or impurity of a dataset. In the context of decision trees, it quantifies the uncertainty associated with the class labels. Information gain, on the other hand, represents the reduction in entropy achieved by partitioning the data based on a specific feature.

import numpy as np

def entropy(y):
    """Calculate the entropy of a dataset."""
    unique, counts = np.unique(y, return_counts=True)
    probabilities = counts / len(y)
    return -np.sum(probabilities * np.log2(probabilities))

def information_gain(y, splits):
    """Calculate the information gain after a split."""
    total_entropy = entropy(y)
    weighted_entropy = sum((len(split) / len(y)) * entropy(split) for split in splits)
    return total_entropy - weighted_entropy

Gini Impurity

Gini impurity measures the probability of misclassifying a randomly chosen element from the dataset. It is calculated similarly to entropy but with a different formula.

def gini_impurity(y):
    """Calculate the Gini impurity of a dataset."""
    unique, counts = np.unique(y, return_counts=True)
    probabilities = counts / len(y)
    return 1 - np.sum(probabilities**2)

4. Decision Tree Algorithms

There are several algorithms for constructing decision trees, with some of the most well-known ones being ID3, C4.5 (C5.0), and CART.

ID3 (Iterative Dichotomiser 3)

ID3, or Iterative Dichotomiser 3, is one of the early decision tree algorithms used for classification. It builds a decision tree in a top-down, recursive manner by selecting the most informative attributes at each node to partition the data. ID3 measures attribute informativeness using “information gain,” which quantifies the reduction in uncertainty (entropy) in the class labels after splitting the data based on an attribute. It’s particularly suited for datasets with categorical attributes and can handle multi-class classification problems. However, ID3 is sensitive to small variations in the data, tends to favor attributes with many categories, and does not handle continuous numeric attributes directly. More advanced algorithms like C4.5 and CART have since evolved to address these limitations while retaining the core concepts of ID3.

C4.5 (C5.0)

C4.5 (also known as C5.0) is a decision tree algorithm developed by Ross Quinlan as an evolution of the earlier ID3 algorithm. It’s designed for both classification and regression tasks. C4.5 uses “gain ratio” as the splitting criterion instead of “information gain,” which helps address the bias of favoring attributes with many categories. This algorithm can handle categorical and continuous numeric attributes, making it more versatile. It also includes a mechanism for handling missing values, making it robust in real-world datasets. C4.5 constructs decision trees by recursively selecting the best attribute to split the data, and it can automatically prune branches to avoid overfitting, leading to more accurate and interpretable models.

CART (Classification and Regression Trees)

CART, or Classification and Regression Trees, is a versatile decision tree algorithm developed by Breiman et al. that can be used for both classification and regression tasks. CART employs “Gini impurity” as the splitting criterion for classification and “mean squared error” for regression, which measures the impurity or error associated with a dataset. It is capable of handling both categorical and continuous numeric attributes, making it suitable for a wide range of datasets. One notable feature of CART is its support for binary splits at each node, meaning it considers only two branches for attribute splits, simplifying the tree structure. Additionally, CART can automatically prune branches based on a cost-complexity measure, helping prevent overfitting and producing simpler and more interpretable trees.

5. Decision Tree Pruning

Decision trees are prone to overfitting, where they capture noise in the data rather than the underlying patterns. Pruning is a technique used to prevent overfitting by removing branches from the tree that do not provide significant predictive power.

Pruning involves setting a maximum depth for the tree, limiting the number of leaf nodes, or defining a minimum number of samples required for a node to be split.

6. Decision Tree in Practice

Let’s see how to implement a decision tree in Python using the scikit-learn library. We’ll use a popular dataset, the Iris dataset, for a simple classification task.

Data Preparation

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

iris = load_iris()
X = iris.data
y = iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Decision Tree in Python

from sklearn.tree import DecisionTreeClassifier

# Create a decision tree classifier
clf = DecisionTreeClassifier(random_state=42)

# Fit the classifier to the training data
clf.fit(X_train, y_train)

# Make predictions on the test data
y_pred = clf.predict(X_test)

Decision Tree Visualization

You can visualize the decision tree using Graphviz or export it as a text representation.

from sklearn.tree import export_text

tree_rules = export_text(clf, feature_names=iris.feature_names)
print(tree_rules)

7. Evaluation of Decision Trees

Evaluating a decision tree model is crucial to assess its performance. Common evaluation metrics include the confusion matrix, accuracy, precision, recall, F1-score, and ROC curves. Cross-validation helps estimate how well the model generalizes to unseen data.

from sklearn.metrics import confusion_matrix, accuracy_score, classification_report

# Evaluate the model
print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))
print("Accuracy:", accuracy_score(y_test, y_pred))
print("Classification Report:\n", classification_report(y_test, y_pred))

8. Advantages and Disadvantages

Advantages of Decision Trees:

Simple to understand and interpret.
Can handle both categorical and numeric data.
Require minimal data preprocessing.
Can be used for feature selection.
Perform well on complex tasks with deep trees.

Disadvantages of Decision Trees:

Prone to overfitting, especially with deep trees.
Sensitive to small variations in the data.
Can create biased trees with imbalanced datasets.
Greedy nature may lead to suboptimal solutions.

9. Conclusion

Decision trees are powerful tools for solving classification and regression problems. They are easy to understand, versatile, and can be a valuable addition to your machine learning toolbox. However, it’s essential to use them wisely,

0 0 votes

Article Rating

Table of Contents