
Hızlı Sıralama (Quick Sort) Rehberi: Böl ve Fethet Algoritması
0 Yorumlar
/
Sıralama, bilgisayar bilimlerinin temel taşlarından biri.…

Birleştirme Sıralaması (Merge Sort) Rehberi: Böl ve Fethet Algoritması
Sıralama, bilgisayar bilimlerinin temel taşlarından biri.…

Dijkstra Algoritması: Python ile Pratik Rehber
Dijkstra Algoritması, 1956’da Hollandalı bilgisayar bilimci…

Birleştirme Sıralaması ve Hızlı Sıralama Rehberi: Böl ve Fethet Algoritmaları
Sıralama, bilgisayar bilimlerinin temel taşlarından biridir…

İkili Arama Algoritması: Verimlilik
Arama, bilgisayar bilimlerinin temel işlemlerinden biridir ve…
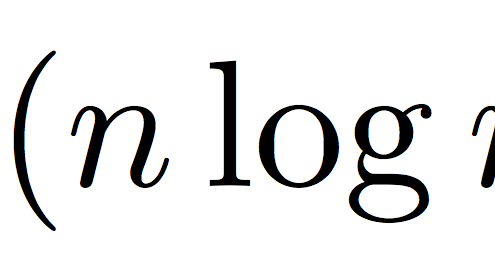
Büyük O Notasyonu Rehberi: Algoritma Verimliliğini Anlama
Algoritmaların verimliliği, bilgisayar bilimleri ve programlama…
