Yazılar

İkili Arama Algoritması: Verimlilik
0 Yorumlar
/
Arama, bilgisayar bilimlerinin temel işlemlerinden biridir ve…
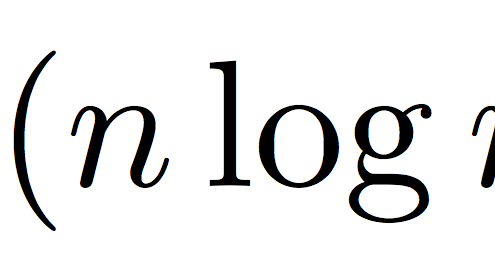
Büyük O Notasyonu Rehberi: Algoritma Verimliliğini Anlama
Algoritmaların verimliliği, bilgisayar bilimleri ve programlama…

Kabarcık Sıralaması Algoritması: Sıralamanın Basitliği
Kabarcık Sıralaması Algoritması: Sıralamanın…

Algoritma: Mantık ve Verimlilik Yolculuğu
Modern teknolojinin karmaşık dokusunda, algoritmalar…
Project Euler – Problem 6 Çözümü
Project Euler’in 6. problemi, matematiksel düşünme ve programlama…

Project Euler – Problem 5 Çözümü
Merhaba! Project Euler’in 5. problemi, hem matematiksel düşünceyi…
