Yazılar

Birleştirme Sıralaması ve Hızlı Sıralama Rehberi: Böl ve Fethet Algoritmaları
0 Yorumlar
/
Sıralama, bilgisayar bilimlerinin temel taşlarından biridir…
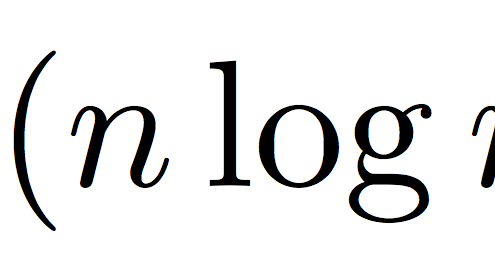
Büyük O Notasyonu Rehberi: Algoritma Verimliliğini Anlama
Algoritmaların verimliliği, bilgisayar bilimleri ve programlama…

Kabarcık Sıralaması Algoritması: Sıralamanın Basitliği
Kabarcık Sıralaması Algoritması: Sıralamanın…

Algoritma: Mantık ve Verimlilik Yolculuğu
Modern teknolojinin karmaşık dokusunda, algoritmalar…

Matematikle Etkili Düşünme: Zihinsel Çeviklik ve Problem Çözme Yeteneğini Geliştirme
Matematik, çoğu zaman zorlayıcı bir akademik disiplin gibi…

Bilgisayar Bilimlerini Öğrenmek İçin Kapsamlı Bir Müfredat
Dijitalleşen dünyamızda bilgisayar bilimlerinin önemi tartışılmaz.…
